Faisabilité d'un problème de Statique : Hyperstatisme et Isostatisme.
Chaque isolement donne 2 équation vectorielles, soit au plus 6 équations scalaires indépendantes.
Un système matériel constitué d'un bâti et de
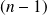solides permet d'écrire
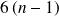équations
Par conséquent, la faisabilité d'un problème de statique dépend du nombre d'inconnues statiques : il faut au plus
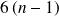inconnues statiques.
Dans ce cas, le problème est dit isostatique. C'est-à-dire qu'on peut le résoudre en utilisant le Principe Fondamental de la Statique.
Si le nombre d'inconnues statiques est plus grand que le nombre d'équations scalaires indépendantes déduites du PFS, le système est dit hyperstatique.
On peut alors calculer le degré d'hyperstatisme d'un système grâce à la relation suivante :
Avec :
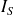: nombre d'inconnues statiques (ou de liaisons)
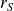: nombre d'équations scalaires indépendantes issues de l'application du PFS
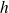: degré d'hyperstatisme.
: nombre de solides composant le système (bâti compris)
Remarque :
On se contente ici d'une inégalité pour
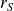. Le calcul exact de ce paramètre ou plus généralement du degré d'hyperstatisme
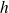sera détaillé en
année dans le cadre de la théorie des mécanismes.
