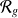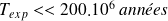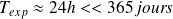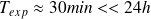C06 : Performances statiques des systèmes - Modéliser, résoudre et expérimenter

Cours

défilement haut

défilement bas

Masquer le plan

Afficher le plan

Principe fondamental de la Statique

Fondamental : Enoncé du Principe Fondamental de la Statique (PFS)

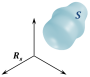Si un système matériel S est en équilibre par rapport à un référentiel galiléen, alors le torseur des actions mécaniques extérieures à S est nul :

$\boxed{ \quad \text{Si S est en équilibre par rapport à un référentiel } R_g \text{ galiléen, alors : } \quad \{ \mathcal T_{\overline S \rightarrow S} \} = \{0\} \quad }$

Remarque :

Attention, la réciproque est fausse : le fait que le torseur des actions mécaniques extérieures à un système matériel soit nul n'implique pas que le système matériel soit à l'équilibre.

Le PFS se traduit par deux équations vectorielles (voir l'exemple ci-après).

Exemple : Bride hydraulique

Principe fondamental de la statique appliqué à la bride 1 en O :

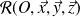Si est en équilibre dans le référentiel supposé galiléen, alors :

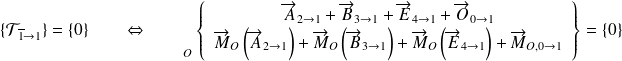
$\begin{array}{c} \{ \mathcal T_{\overline 1 \rightarrow 1} \}= \{0\} \quad \quad \Leftrightarrow \quad \quad {\vphantom{\left\{\begin{array}{ccc}\overrightarrow{R_{2\rightarrow 1}} \\\overrightarrow{M_{A} (2\rightarrow 1)}\end{array}\right\}}} _{O} \left \{ \begin{array}{c} \overrightarrow{A}_{2 \rightarrow 1 } +\overrightarrow{B}_{3 \rightarrow 1 } +\overrightarrow{E}_{4 \rightarrow 1 } +\overrightarrow{O}_{0 \rightarrow 1 } \\ \overrightarrow{M}_{O}\left( \overrightarrow{A}_{2 \rightarrow 1 }\right)+\overrightarrow{M}_{O}\left( \overrightarrow{B}_{3 \rightarrow 1 }\right)+\overrightarrow{M}_{O}\left( \overrightarrow{E}_{4 \rightarrow 1 }\right)+\overrightarrow{M}_{O, 0\rightarrow 1 } \end{array} \right \} = \{0\} \end{array}$

On obtient ainsi les 2 équations vectorielles suivantes :

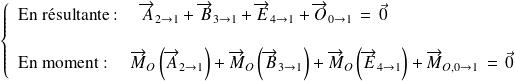
$\left\{ \begin{array}{l} \text{En résultante : } \quad \overrightarrow{A}_{2 \rightarrow 1 } +\overrightarrow{B}_{3 \rightarrow 1 } +\overrightarrow{E}_{4 \rightarrow 1 } +\overrightarrow{O}_{0 \rightarrow 1 }\, = \, \vec0 \\ \\ \text{En moment : }\quad \overrightarrow{M}_{O}\left( \overrightarrow{A}_{2 \rightarrow 1 }\right)+\overrightarrow{M}_{O}\left( \overrightarrow{B}_{3 \rightarrow 1 }\right)+\overrightarrow{M}_{O}\left( \overrightarrow{E}_{4 \rightarrow 1 }\right)+\overrightarrow{M}_{O, 0\rightarrow 1 }\, = \, \vec0 \end{array} \right.$

Théorème de la résultante statique

Fondamental : Théorème de la résultante statique appliqué à S

$\boxed{\quad \text{Si S est en équilibre par rapport à un référentiel } R_g \text{ galiléen, alors : } \quad \overrightarrow R_{\overline S \rightarrow S}=\vec 0 \quad}$

Remarque :

En projetant cette équation vectorielle dans le repère spatial associé au référentiel, on obtient 3 équations scalaires.

Exemple : Bride hydraulique

Théorème de la résultante statique appliqué à la bride 1:

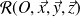Si est en équilibre dans le référentiel supposé galiléen, alors :

$\overrightarrow{R}_{\overline 1\rightarrow 1 } = \vec 0 \quad \Leftrightarrow \quad \overrightarrow{A}_{2\rightarrow 1 } +\overrightarrow{B}_{3 \rightarrow 1 } +\overrightarrow{E}_{4 \rightarrow 1 } +\overrightarrow{O}_{0 \rightarrow 1 }=\vec 0 \\$

Par projection dans la base 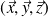associée à , on obtient :

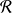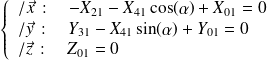
$\left\{ \begin{array}{l} /\vec x\, :\quad-X_{21}-X_{41}\cos(\alpha) +X_{01} =0 \\ /\vec y\, :\quad Y_{31}-X_{41}\sin(\alpha)+Y_{01}=0 \\ /\vec z\, :\quad Z_{01} =0 \end{array} \right.$

Théorème du moment statique

Fondamental : Théorème du moment statique appliqué à S au point P

$\boxed{\quad \text{Si S est en équilibre par rapport à un référentiel } R_g \text{ galiléen, alors : } \quad \overrightarrow M_{P,\,\overline S \rightarrow S}=\vec 0 \quad}$

Remarque :

De même, en projetant cette équation vectorielle dans le repère spatial associé au référentiel, on obtient 3 équations scalaires.

Attention :

Ne pas oublier de toujours bien préciser le point choisi pour l'application du théorème du moment statique.

Exemple : Bride hydraulique

Théorème du moment statique appliqué à la bride 1 en O :

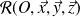Si est en équilibre dans le référentiel supposé galiléen, alors :

$\overrightarrow{M}_{O,\overline 1\rightarrow 1 } = \vec 0 \, \Leftrightarrow \quad\overrightarrow{M}_{O}\left( \overrightarrow{A}_{2 \rightarrow 1}\right)+\overrightarrow{M}_{O}\left( \overrightarrow{B}_{3 \rightarrow 1 }\right)+\overrightarrow{M}_{O}\left( \overrightarrow{E}_{4 \rightarrow 1}\right)+\overrightarrow{M}_{O, 0\rightarrow 1 }=\vec0$

Par projection dans la base 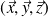associée à , on obtient :

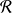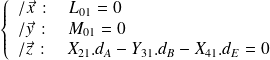
$\left\{ \begin{array}{l} /\vec x\, : \quad L_{01}=0 \\ /\vec y\, : \quad M_{01}=0 \\ /\vec z\, : \quad X_{21}.d_A -Y_{31}.d_B-X_{41}.d_E=0 \end{array} \right.$

Complément sur la notion de référentiel galiléen

Définition :

On appelle référentiel galiléen un référentiel dans lequel le PFS est vérifié.

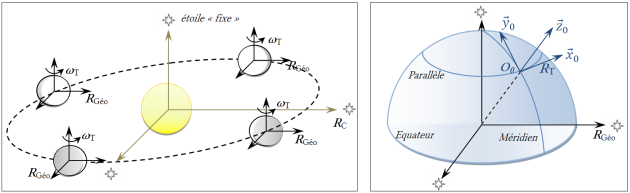
La notion de référentiel galiléen est absolue, c'est à dire que le repère spatial est considéré comme "fixe" par rapport à l'ensemble de l'Univers au cours du temps. En toute rigueur, un tel référentiel n'existe pas.

Cependant, pour les systèmes étudiés, il pourra être admis que les référentiels suivants restent de bonnes approximations de référentiels galiléens :

Type de référentiel	Origine	Axes
Référentiel de Copernic	Centre de masse du système solaire (proche de celui du Soleil)	Dirigés vers 3 étoiles fixes
Référentiel géocentrique (ou de Foucault)	Centre de masse de la Terre	Dirigés vers 3 étoiles fixes
Référentiel terrestre (ou du laboratoire)	Lié à la surface terrestre	Fixes par rapport à la Terre

Type de référentiel

Origine

Axes

Validité

Référentiel de Copernic

Centre de masse du système solaire

(proche de celui du Soleil)

Dirigés vers 3 étoiles fixes