C06 : Performances statiques des systèmes - Modéliser, résoudre et expérimenter

Cours

défilement haut

défilement bas

Masquer le plan

Afficher le plan

Cas particulier des problèmes plans

Simplification plane

Fondamental : Simplification plane

Si le système étudié admet un plan de symétrie géométrique qui est aussi plan de symétrie pour les actions mécaniques extérieures (symétrie de charge), on dit que le problème est plan.

La simplification plane nous conduit à résoudre un problème dans lequel :

les forces sont contenues dans le plan de symétrie,

les moments sont perpendiculaires au plan de symétrie.

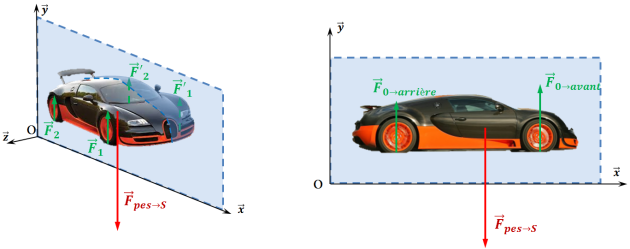
Exemple : Cas d'un véhicule en équilibre

le plan 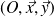est un plan de symétrie géométrique du véhicule,

les efforts 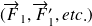sont symétriques par rapport à ce plan.

On peut donc supposer que le problème est plan dans le plan 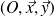et se ramener au cas de la figure de droite. Attention tout de même dans les calculs à tenir compte du fait que les efforts 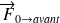et 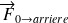correspondent aux efforts cumulés exercés par le sol respectivement sur les roues avant et arrières :

$\overrightarrow F_{0 \rightarrow avant}=\overrightarrow F_1+\overrightarrow F_1'=2 \, \overrightarrow F_1 \quad \quad \text{et} \quad \quad \overrightarrow F_{0 \rightarrow arriere}=\overrightarrow F_2+\overrightarrow F_2'= 2 \, \overrightarrow F_2$

Fondamental : Conséquences

Dans le cas d'un problème plan dans le plan 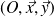, tous les torseurs des A.M s'écrivent sous la forme suivante :

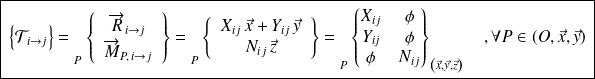
$\boxed{ \,\left \{ \mathcal T_{i \rightarrow j} \right \} = {\vphantom{\left\{\begin{array}{ccc} \overrightarrow{R_{2\rightarrow 1}} \\ \overrightarrow{M_{A} (2\rightarrow 1)} \end{array}\right\}}} _{P} \left \{ \begin{array}{c} \overrightarrow{R}_{i \rightarrow j } \\ \overrightarrow{M}_{P,\, i \rightarrow j } \end{array} \right \} = {\vphantom{\left\{\begin{array}{ccc} \overrightarrow{R_{2\rightarrow 1}} \\ \overrightarrow{M_{A} (2\rightarrow 1)} \end{array}\right\}}} _{P} \left \{ \begin{array}{c} X_{ij}\,\vec x +Y_{ij}\,\vec y\\ N_{ij}\,\vec z \\ \end{array} \right \} = {\vphantom{ \left \{ \begin{matrix} X_{21} & L_{21} \\ Y_{21} & M_{21} \\ Z_{21} & N_{21} \\ \end{matrix} \right \} }} _{P} \left \{ \begin{matrix} X_{ij} & \phi \\ Y_{ij} & \phi \\ \phi & N_{ij} \\ \end{matrix} \right \}_{\left( \vec x, \vec y, \vec z \right)} \quad, \forall P\in (O,\vec x, \vec y) \, }$

Les composantes 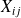, 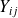et 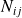peuvent éventuellement être nulles.
Les composantes 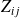, 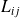et 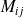sont nécessairement nulles du fait du problème plan dans le plan .

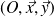Remarque :

L'application du PFS dans le cadre d'un problème plan donne 3 équations à résoudre :

2 équations provenant du Théorème de la Résultante Statique (projection de l'égalité vectorielle sur chacun des 2 axes du plan de la feuille)

1 équation provenant du Théorème du Moment Statique (projection sur l'axe perpendiculaire au plan de la feuille).

En projetant cette équation vectorielle dans le repère spatial associé au référentiel, on obtient 3 équations scalaires.

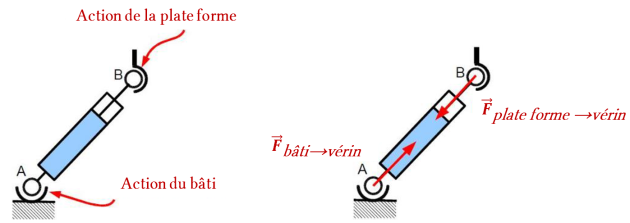
Exemple : Bride hydraulique

En considérant le problème plan dans le plan 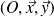, on peut simplifier les torseur de chacune des actions mécaniques extérieures à la bride 1:

action mécanique du piston 2→ 1 :
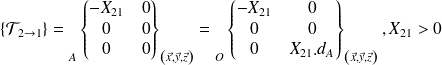(pas de modification)
action mécanique de 3 → 1 :
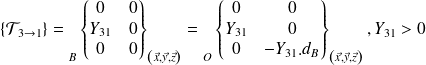(pas de modification)

action mécanique de 4 → 1 :
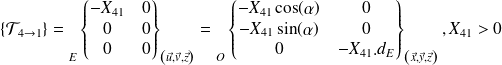(pas de modification)

action mécanique du bâti 0→ 1 en O :

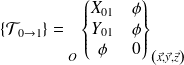
Théorème de la résultante statique appliqué à la bride 1 :

Si est en équilibre dans le référentiel supposé galiléen, alors :

$\overrightarrow{R}_{\overline 1\rightarrow 1 } = \vec 0 \quad \Leftrightarrow \quad \overrightarrow{A}_{2\rightarrow 1 } +\overrightarrow{B}_{3 \rightarrow 1 } +\overrightarrow{E}_{4 \rightarrow 1 } +\overrightarrow{O}_{0 \rightarrow 1 }=\vec 0 \\$

Par projection dans la base liée à , on obtient :

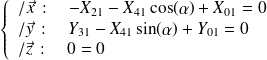
$\left\{ \begin{array}{l} /\vec x\, : \quad -X_{21}-X_{41}\cos(\alpha) +X_{01} =0 \\ /\vec y\, : \quad Y_{31}-X_{41}\sin(\alpha)+Y_{01}=0 \\ /\vec z\, : \quad 0 =0 \end{array} \right.$

Théorème du moment statique appliqué à la bride 1 en O :

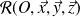Si est en équilibre dans le référentiel supposé galiléen, alors :

$\overrightarrow{M}_{O,\overline 1\rightarrow 1 } = \vec 0 \, \Leftrightarrow \quad\overrightarrow{M}_{O}\left( \overrightarrow{A}_{2 \rightarrow 1}\right)+\overrightarrow{M}_{O}\left( \overrightarrow{B}_{3 \rightarrow 1 }\right)+\overrightarrow{M}_{O}\left( \overrightarrow{E}_{4 \rightarrow 1}\right)+\overrightarrow{M}_{O, 0\rightarrow 1 }=\vec0$

Par projection dans la base 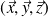liée à , on obtient :

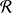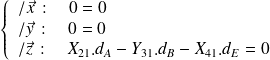
$\left\{ \begin{array}{l} /\vec x\, : \quad 0=0 \\ /\vec y\, : \quad 0=0 \\ /\vec z\, : \quad X_{21}.d_A -Y_{31}.d_B-X_{41}.d_E=0 \end{array} \right.$

Conclusions :

L'équation issue du TMS appliqué à la bride 1 en O nous donne une relation entrée-sortie en effort. On peut ici donner l'expression de l'effort recherché du vérin sur la bride en fonction de l'effort de serrage 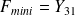imposé en B :

$\boxed{X_{21} = \frac {F_{mini}.d_B+ X_{41}.d_E}{d_A}} \quad \quad (\text{dépend aussi de l'effort }X_{41} \text{induit par l'action du ressort 5 sur 4})$

On remarque que les équations issue du TRS appliqué à la bride 1 permettent de déterminer les inconnues de liaison en O : 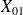et 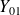. Ces données permettraient par exemple, dans le cadre d'une étude de conception de choisir et de dimensionner les composants participant à la réalisation de la liaison pivot d'axe .

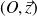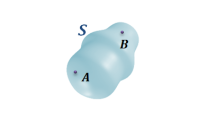
Cas d'un solide en équilibre soumis à deux glisseurs - Application graphique

Soit S un système matériel en équilibre soumis à deux glisseurs :

de la part d'un solide appliqué au point A :

de la part d'un solide appliqué au point B :

Appliquons le PFS à {S} :

Théorème de la résultante statique appliqué à S :
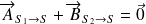
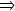les deux forces ont même direction, même norme et sont de sens opposés.

Théorème du moment statique appliqué à S au point A :

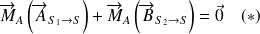
Or 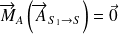et
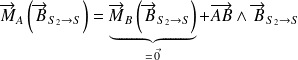
Donc

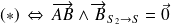
Ainsi, 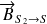est colinéaire à 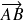et donc 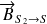a pour support la droite .

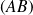Enfin, comme 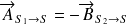, 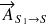a également pour support la droite .

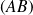Fondamental :

Si un système matériel soumis à deux glisseurs en A et B est en équilibre alors, les résultantes :

ont même support : la droite ;

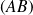ont même norme ;

sont de sens opposés.

Exemple : équilibre d'un vérin de l'hexapode (version hydraulique), poids négligé

Cas d'un solide en équilibre soumis à trois glisseurs - Application graphique

Pour résoudre le cas de l'équilibre d'un système soumis à 3 glisseurs, il faut connaître au minimum :

une force entièrement (direction, sens et norme) ;

le support d'une des deux autres forces.

Ainsi vous êtes en mesure de distinguer deux cas :

si les deux directions connues ne sont pas parallèles, alors on se trouve dans le cas général d'un système soumis à 3 forces non parallèles.

si les deux directions connues sont parallèles, alors la troisième force est nécessairement parallèle aux deux autres et on se trouve dans le cas particulier d'un système soumis à 3 forces parallèles

Cas d'un solide en équilibre soumis à trois glisseurs non parallèles

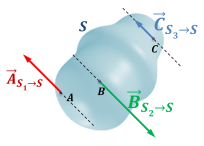
Soit S un système matériel en équilibre soumis à trois glisseurs :

de la part d'un solide 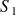appliqué au point A :

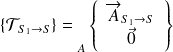
de la part d'un solide 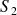appliqué au point B :

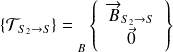
de la part d'un solide 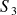appliqué au point C :

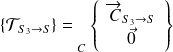
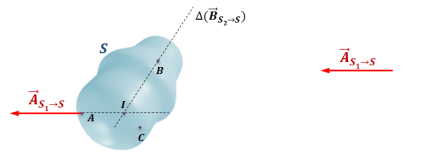
Appliquons le PFS à {S} :

Théorème de la résultante statique appliqué à S :
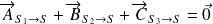
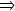la somme vectorielle des 3 forces est nulle : elles sont coplanaires et le triangle des forces est fermé.

Théorème du moment statique appliqué à S au point I, point d'intersection des supports 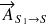de et de :

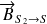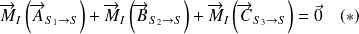
Or 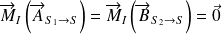puisque I se trouve sur les supports 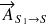de et de .
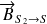Ainsi,
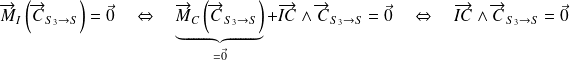
Donc 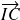et 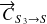sont colinéaires
Donc le support de 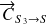passe aussi par le point I
Donc les supports des 3 forces sont concourants.

Fondamental :

Si un système matériel est en équilibre sous l'action de glisseurs (de résultantes non parallèles), alors les résultantes de ces glisseurs sont :

concourantes (leurs supports se coupent en un même point) ;

coplanaires ;

de somme vectorielle nulle (le triangle des forces est fermé).

Remarque : Application graphique

Connaissant une force entièrement et le support d'une seconde force, il est possible de construire le triangle des forces (ou dynamique) et de déterminer complètement et graphiquement les trois forces.

Exemple : équilibre d'un vérin de l'hexapode (version hydraulique), poids non négligé

Cas d'un solide en équilibre soumis à trois glisseurs (3 forces) parallèles

Fondamental :

Si un système matériel est en équilibre sous l'action de glisseurs (de résultantes parallèles), alors les résultantes de ces glisseurs sont :

parallèles ;

coplanaires ;

de somme vectorielle nulle.

Dans ce cas, il convient d'utiliser une méthode de résolution analytique consistant, selon les données de l'énoncé, à appliquer le TRS et/ou le TMS en un point judicieusement choisi.

Accueil

Imprimer